Gerak parabola

Sumber : id.wikibooks.com

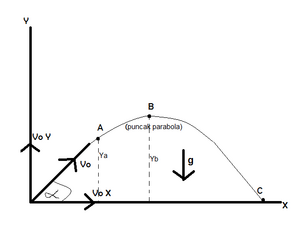
Gerak parabola adalah gerak yang membentuk sudut tertentu terhadap bidang horizontal. Pada gerak parabola, gesekan diabaikan, dan gaya yang bekerja hanya gaya berat/percepatan gravitasi.

Pada titik awal,

${\displaystyle Vo_{x}=Vo\times \cos \alpha }$

${\displaystyle Vo_{y}=Vo\times \sin \alpha }$

Pada titik A (t = t_a):

${\displaystyle Va_{x}=Vo_{x}=Vo\times \cos \alpha }$

${\displaystyle Va_{y}=Vo_{y}-g\times t_{a}}$

Letak/posisi di A:

${\displaystyle X_{a}=Vo_{x}\times t_{a}}$

${\displaystyle Y_{a}=Vo_{y}\times t_{a}-1/2g{t_{a}^{2}}}$

Titik tertinggi yang bisa dicapai (B):

${\displaystyle h_{max}={\frac {{(Vo\times \sin \alpha })^{2}}{2g}}={\frac {{(Vo^{2}\times \sin ^{2}\alpha })}{2g}}}$

Waktu untuk sampai di titik tertinggi (B) (t_b):

${\displaystyle V_{y}=0}$

${\displaystyle V_{y}=Vo_{y}-gt}$

${\displaystyle 0=Vo\sin \alpha -gt}$

${\displaystyle t_{b}={\frac {{(Vo\times \sin \alpha })}{g}}={\frac {Vo_{y}}{g}}}$

Jarak mendatar/horizontal dari titik awal sampai titik B (Xb):

${\displaystyle X_{b}=Vo_{x}\times t_{b}}$

${\displaystyle X_{b}=Vo\cos \alpha \times ({\frac {{(Vo\times \sin \alpha })}{g}})}$

${\displaystyle X_{b}={\frac {{Vo^{2}}\times \sin 2\alpha }{2g}}}$

Jarak vertikal dari titik awal ke titik B (Yb):

${\displaystyle Y_{b}={\frac {Vo_{y}^{2}}{2g}}}$

${\displaystyle Y_{b}={\frac {{Vo^{2}}\times \sin ^{2}\alpha }{2g}}}$

Waktu untuk sampai di titik C:

${\displaystyle t_{total}={\frac {{(2Vo\times \sin \alpha })}{g}}={\frac {2Vo_{y}}{g}}}$

Jarak dari awal bola bergerak sampai titik C:

${\displaystyle X_{maks}=Vo{x}\times t_{total}}$

${\displaystyle X_{maks}=Vo\times \cos \alpha \times {\frac {{(2Vo\times \sin \alpha })}{g}}}$

${\displaystyle X_{maks}={\frac {{Vo^{2}}\times \sin 2\alpha }{g}}}$